1 patarimas. Kaip apskaičiuoti skaičiaus modulį
1 patarimas. Kaip apskaičiuoti skaičiaus modulį
Modulis skaičius Ar absoliuti vertė yra parašyta vertikaliais skliaustuose: | x |. Jis gali būti vizualizuotas kaip intervalas, išdėstytas bet kuria kryptimi nuo nulio.

Instrukcijos
1
Jei modulis pateikiamas kaip tęstinisfunkcija, jos argumentas gali būti teigiamas arba neigiamas: | x | = x, x ≥ 0; | x | = - x, x <0. Taigi, skliausteliuose įterptas skaičius užima bet kokį ženklą.
2
Nulinis modulis yra nulinis, o bet kurio modulio modulisteigiamas skaičius jam. Jei argumentas yra neigiamas, po skliaustuose atskleidimo keičia savo ženklą iš minuso į pliuso. Remiantis tuo, darytina išvada išplaukia, kad moduliai priešingi skaičiai yra lygūs: | -x | = | x | = x
3
Kompleksinio skaičiaus modulis randamas pagal formulę: | a |. | = √b ² + c ², ir | a + b | ≤ | a | + | b |. Jei argumentas turi teigiamą sveikąjį skaičių kaip daugiklį, jis gali būti paimtas už ženklo bracket, pavyzdžiui: | 4 * b | = 4 * | b |.
4
Modulis negali būti neigiamas, todėl bet koks neigiamas skaičius yra konvertuojamas į teigiamą: | -x | = x, | -2 | = 2; | -1/7 | = 1/7, | -2.5 | = 2,5
5
Jei argumentas pateikiamas kaip sudėtingas skaičius,tada skaičiavimo patogumui leidžiama keisti išraiškos, išdėstytos stačiakampiuose skliaustuose, eiliškumo tvarka: | 2-3 | = | 3-2 | = 3-2 = 1, nes (2-3) yra mažesnis nei nulis.
6
Pakeliamos argumentas tuo pačiu metu yra prie to paties, kad šaknies ženklu - ji išspręsta su modulio pagalba: √a² = | A | = ± a.
7
Jei turite užduotį, kuri nėra įtrauktamodulio skliausteliams išplėsti reikalingą sąlygą, nereikia jų atsikratyti - tai bus galutinis rezultatas. Ir jei norite juos atskleisti, turite nurodyti ženklą ±. Pavyzdžiui, jums reikia rasti išraiškos reikšmę √ (2 * (4-b)) ². Jo sprendimas atrodo taip: √ (2 * (4-b)) ² = | 2 * (4-b) | = 2 * | 4-b |. Kadangi žodžio 4-b ženklas nežinoma, jis turi būti paliktas skliausteliuose. Jei pridedame papildomą sąlygą, pavyzdžiui, | 4-b | > 0, tada galiausiai gauname 2 * | 4-b | = 2 * (4 - b). Kaip nežinomas elementas, taip pat galima nurodyti konkretų skaičių, į kurį reikėtų atsižvelgti, nes tai paveiks išraiškos ženklą.
2 patarimas. Kaip rasti numerio modulį
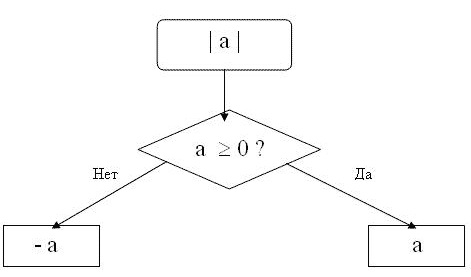
Modulis skaičius n - vienetų segmentų skaičius nuo kilmės iki taško n. Ir nesvarbu, kokia kryptimi šis atstumas bus matuojamas - nuliui į dešinę arba į kairę.
Instrukcijos
1
Modulis skaičius taip pat vadinamas absoliučia šio vertės reikšme skaičius. Tai žymi trumpos vertikalios linijos, nukreiptos į kairę ir dešinę skaičius. Pavyzdžiui, modulis skaičius 15 parašyta taip: | 15 |.
2
Atminkite, kad modulis gali būti tik teigiamas skaičius arba nulis. Modulis teigiamas skaičius yra lygus pačiam skaičiui. Modulis nulis yra lygus nuliui. Tai yra bet kokia skaičius n, kuris yra didesnis arba lygus nuliui, bus tokia formulė: | n | = n Pavyzdžiui, | 15 | = 15, t. Y. Modulis skaičius 15 yra lygus 15.
3
Neigiamas skaičius bus tas pats numeris, bet su priešais ženklas. Tai yra bet kokia skaičius n, kuris yra mažesnis nei nulis, formulė | n | = -n. Pavyzdžiui, | -28 | = 28 Modulis skaičius -28 yra lygus 28.
4
Modulius galite rasti ne tik sveikiems skaičiams, bet ir trupmeniniams skaičiams. Tos pačios taisyklės taikomos ir trupmeniniams skaičiams. Pavyzdžiui, | 0,25 | = 25, ty modulis skaičius 0,25 bus lygus 0,25. | -2 | = ¾, tai yra, modulis skaičius -¾ bus lygus ¾.
5
Kai dirbate su moduliais, naudinga žinoti, kad priešingų skaičių moduliai visada vienodi, tai yra, | n | = | -n |. Tai yra pagrindinė modulių savybė. Pavyzdžiui, | 10 | = | -10 |. Modulis skaičius 10 yra 10, kaip ir modulis skaičius -10. Be to, | a - b | = | b - a |, nes atstumas nuo taško a iki b punkto ir atstumas nuo b iki a yra vienodai vienodi. Pavyzdžiui, | 25 - 5 | = | 5 - 25 |, tai yra, | 20 | = | - 20 |.
3 patarimas. Kaip apskaičiuoti sudėtingus skaičius
Sudėtingi skaičiai - tolesnis koncepcijos išplėtimasskaičiai, palyginti su realiais skaičiais. Įvadas į sudėtingų skaičių matematiką leido pateikti galutinę formulę daugeliui įstatymų ir formulių, taip pat atskleidė gilius ryšius tarp skirtingų matematinių mokslų sričių.

Instrukcijos
1
Kaip žinoma, nėra tikro skaičiausgali būti kvadratinė šaknis iš neigiamo skaičiaus, ty jei b <0, tada neįmanoma rasti a tokį, kad a ^ 2 = b. Todėl buvo nuspręsta įvesti naują vienetą, kuriuo galėtume išreikšti tokį. Jis vadinamas įsivaizduojamu vienetu ir užrašu i. Vaizdinis vienetas yra lygus kvadratinei šakniai iš -1.
2
Kadangi i ^ 2 = -1, tai reiškia, kad √ (-b ^ 2) = √ ((- 1) * b ^ 2) = √ (-1) * √ (b ^ 2) = ib. Taigi įvesta įsivaizduojamo skaičiaus sąvoka. Bet koks įsivaizduojamas skaičius gali būti išreikštas kaip ib, kur b yra tikras skaičius.
3
Realieji skaičiai gali būti pateikti formojeskaitinė ašis nuo minus begalybės iki plius begalybės. Patogiai reprezentuoti įsivaizduojamą skaičių formą, analogišką ašiai, statmenai realių skaičių ašiai. Kartu jie sudaro skaitmeninius koordinates kiekviename taške ploskosti.Pri Ši skaitinė plokštuma su koordinačių (a, b) atitinka vienas ir tik vienas kompleksinio skaičiaus formos A + IB, kur a ir b - yra realieji skaičiai. Pirmasis šios sumos terminas vadinamas realia sudėtinio skaičiaus dalimi, o antroji terminas vadinama įsivaizduojama dalimi.
4
Jei a = 0, tada kompleksinis skaičius vadinamas grynaja įsivaizduojama. Jei b = 0, tada numeris vadinamas realiu.
5
Papildymo ženklas tarp tikro ir įsivaizduojamosudėtingo skaičiaus dalys nereiškia jų aritmetinės sumos. Vietoj to kompleksinis numeris gali būti pateikiamas kaip vektorius, kurio kilmė sutampa su kilme, o galas yra (a, b). Kaip ir bet kuriame vektoriuje, kompleksinis skaičius turi absoliučią vertę arba modulį. Jei z = x + iy, tada | z | = √ (x2 + y ^ 2).
6
Du kompleksiniai skaičiai yra lygūs tikjei tikra dalis lygi tikrosioms dalis ir įsivaizduojama dalimi kita yra įsivaizduojama dalis, kita vertus, tai yra: Z1 = Z2, jei X1 = X2 ir Y1 = y2.Odnako už kompleksinių skaičių neturi prasmės nelygybės požymių, kad tai nereiškia, kad Z1 <Z2 ir Z1> Z2. Tokiu būdu galite palyginti sudėtingų skaičių modulius.
7
Jei z1 = x1 + iy1 ir z2 = x2 + iy2 yra sudėtinginumeriai, tada: Z1 + z2 = (x1 + x2) + I (Y1 + y2); Z1 - Z2 = (x1 - X2) + I (Y1 - Y2); lengva pamatyti, kad pridedant ir atimties kompleksinių skaičių taip tas pats taisyklė, kad vektorių pridėjimas ir atimtis.
8
Dviejų kompleksinių skaičių produktas lygus: Z1 * Z2 = (x1 + iy1) * (x2 + iy2) = x1 * X2 + I * Y1 * X2 + i * x1 * Y2 + (I ^ 2) * Y1 * i y2.Poskolku ^ 2 = -1, tada galutinis rezultatas yra: (X1 X2 * - Y1 * Y2) + I (X1 * Y2 + X2 * Y1).
9
Eksponavimo operacijos ir šaknies ištraukimasuž sudėtingus skaičius yra apibrėžiami taip pat kaip ir realių skaičių. Tačiau, kompleksinės srityje, kad bet kokį skaičių egzistuoja lygiai n tokiais kiekiais, kad b b ^ n = a, t.y. n n-oji šaknys stepeni.V ypač, tai reiškia, kad bet algebrinė lygtis n-oji laipsnis vienas kintamasis turi lygiai n sudėtingos šaknys, iš kurių kai kurios gali būti galiojančios.
4 patarimas. Kaip pridėti numerį prie šaknies
Šaknis yra piktogramamatematinė operacija - surasti tokį skaičių, kurio pastatymas iki žymens, nurodyto prie šaknies ženklo, turėtų būti nurodytas pagal šį ženklą nurodytu numeriu. Dažnai sprendžiant problemas, kuriose yra šaknų, nepakanka tik apskaičiuoti vertę. Mes turime atlikti papildomas operacijas, iš kurių vienas yra skaitinio, kintamojo ar išraiškos pridėjimas prie šaknies ženklo.

Instrukcijos
1
Nustatykite šaknies eksponentą. Indeksas yra sveikas skaičius, rodantis, kiek reikia šaknies skaičiavimo rezultato pakelti, norint gauti šaknies išraišką (skaičių, iš kurio šitas šaknis išgaunamas). Šaknies ekspozicija yra užrašyta viršutiniu indeksu prieš šaknies simbolį. Jei šis indeksas nenurodytas, tai yra kvadratinis šaknis, kurio laipsnis yra du. Pavyzdžiui, šakninis indeksas √3 yra lygus dviems, indeksas ³√3 yra lygus trims, pagrindinis rodiklis √√3 lygus keturiems ir tt
2
Padidinkite numerį, kurį norite pateiktišaknies ženklas, galia, lygi šio šaknies eksponentui, kaip nustatė ankstesnis žingsnis. Pavyzdžiui, jei norite įvesti numerį 5 po šaknies ženklu ⁴√3, tada šaknies ekspozicija yra keturi, o jums reikia apskaičiuoti 5 pastatymo į ketvirtąją galią rezultatą 5,4 = 625. Galite tai padaryti bet kuriuo patogiu būdu - jūsų galvoje, naudodamiesi skaičiuotuvu ar atitinkamomis internetinėmis paslaugomis, pateiktomis internete.
3
Įveskite vertę, gautą ankstesniame etapepo šaknies ženklu kaip raiškos ir išraiškos daugiklis. Pavyzdžiui, naudojamame ankstesniame žingsnyje, prie šaknies ⁴√3 pridedant 5 (5 * ⁴√3), šis veiksmas gali būti parašytas taip: 5 * ⁴√3 = ⁴√ (625 * 3).
4
Supaprastinkite išvestą radikalą, jeitai įmanoma. Dėl ankstesnių etapų Pavyzdžiui, tai reiškia, kad jums tiesiog reikia padauginti skaičių stovėti prie šaknų ženklą: 5 * ⁴√3 = ⁴√ (625 * 3) = ⁴√1875. Šioje priėmimo šaknų skaičių operacija yra baigta.
5
Jei problemoje yra nežinomųkintamieji, pirmiau aprašyti veiksmai gali būti atliekami bendrai. Pavyzdžiui, jei norite, kad ketvirtą šaknį nežinomų kintamųjų x, radikali išraiška yra lygi 5 / X ³, visa veiksmų seka gali būti parašytas kaip: X * ⁴√ (5 / X ³) = ⁴√ (x⁴ * 5 / X ³) = ⁴√ (x * 5).
5 patarimas. Kaip rasti sudėtingo skaičiaus modulį
Realių skaičių nepakankaišspręsti bet kokią kvadratiną lygtį. Paprasčiausias kvadratines lygtis, neturintis šaknies tarp realių skaičių, yra x ^ 2 + 1 = 0. Spręsdamas, pasirodo, kad x = ± sqrt (-1), o pagal elementariosios algebra įstatymus išgauti netgi laipsnio šaknį iš neigiamos skaičius tai neįmanoma.
Jums reikės
- - popierius;
- - rankena.
Instrukcijos
1
Šiuo atveju yra du būdai: Pirmasis - laikytis nustatytų draudimų ir manyti, kad tai lygtis turi šaknis nėra; antrasis - išplėsti realiųjų skaičių sistemą tiek, kiek, kad lygtis turės sąvoka kornem.Tak sudėtingus numerius forma z = A + Ib, kurioje (I ^ 2) = - 1, kur i - menamas vienetas. Skaičiai a ir b yra vadinamas, atitinkamai, realus ir įsivaizduojamas dalys skaičius z Rez ir Imz. Svarbus vaidmuo vykdant sudėtingus veiksmus skaičiusžaidžia skaičius kompleksinis konjugatas. Konjugatas prie kompleksinio skaičiaus z = a + ib vadinamas zs = a-ib, tai yra skaičius, turintis priešingą ženklą prieš įsivaizduojamą vienetą. Taigi, jei z = 3 + 2i, tada zs = 3-2i. Bet koks realus skaičius yra konkretus komplekso atvejis skaičius, kurio įsivaizduojama dalis yra nulis. 0 + i0 yra kompleksinis skaičius, lygus nuliui.
2
Išsami skaičius gali būti pridedamas ir padauginamas taip pat kaip irdaryti su algebinėmis išraiškomis. Tuo pačiu metu galioja ir įprasti papildymo ir dauginimo įstatymai. Tegul z1 = a1 + ib1, z2 = a2 + ib2.1. Be to, ir vychitanie.z1 + z2 = (A1 + A2) + I (b1 + b2), Z1-Z2 = (A1-A2) + I (B1-B2). 2. Umnozhenie.z1 * Z2 = (A1 + IB1) (a2 + IB2) = a1a2 + ia1b2 + ia2b1 + (I ^ 2) b1b2 = (a1a2-b1b2) + I (a1b2 + a2b1) .Jei dauginama tiesiog atidaryti skliausteliuose ir taikykite apibrėžtį i ^ 2 = -1. Produktas konjugatas kompleksinis skaičius yra realus numeris: Z * ZS = (a + IB) (a-IB) == A ^ 2- (I ^ 2) (b ^ 2) = A ^ 2 + b ^ 2.
3
3. skyrius.Kad asmeninįpranešimą Z1 / Z2 = (A1 + IB1) / (a2 + ib2), kad standartinės formos atsikratyti įsivaizduojamo vieneto vardiklį. Už tai lengviausia dauginti skaitiklį ir vardiklį konjuguota vardiklį: ((A1 + IB1) (A2-ib2)) / ((A2 + IB2) (A2-IB2)) = ((a1a2 + b1b2) + I (a2b1 -a1b2)) / (a + b ^ 2 ^ 2) = = (a1a2 + b1b2) / (a + b ^ 2 ^ 2) + I (a2b1-a1b2) / (a + b ^ 2 ^ 2) .Operatsii sudėties ir atimties taip pat daugyba ir dalyba yra tarpusavyje atvirkštinė.
4
5
Su kiekvienu kompleksinės plokštumos tašku z šio taško spindulys vektorius yra prijungtas. Spinduliu vektoriaus ilgis, reprezentuojantis kompleksinį skaičių z, vadinamas moduliu r = | z | integruotas skaičius; o kampas tarp teigiamos tikros ašies krypties ir vektoriaus 0Z kryptės vadinamas šio komplekso argz argumentu skaičius.
6
Komplekso argumentas skaičius yra laikomas teigiamu, jei jis skaičiuojamas nuoteigiama 0x ašies kryptis prieš laikrodžio rodyklę, o neigiama - priešinga kryptimi. Vienas kompleksinis skaičius atitinka argumento argz + 2nk reikšmių rinkinį. Iš šių verčių argozo reikšmės, esančios nuo -n iki n, laikomos pagrindinėmis. Konjugato kompleksas skaičius Z ir ZS turi vienodus modulius, o jų argumentai yra vienodi absoliučia verte, tačiau skiriasi ženkle.
7
Taigi, | z | ^ 2 = a ^ 2 + b ^ 2, | z | = sqrt (a ^ 2 + b ^ 2). Taigi, jei z = 3-5i, tada | z | = sqrt (9 + 25) = 6. Be to, kadangi z * zs = | z | ^ 2 = a ^ 2 + b ^ 2, įmanoma apskaičiuoti visus sudėtingus išraiškos modulius, kuriuose įsivaizduojamas vienetas gali pasirodyti pakartotinai. Kadangi z = (1-3i) ( 4 + i) / (2-2i) = 9/2-i, tiesioginis skaičiavimas modulio z suteikia | z | ^ 2 = 81/4 + 1 = 85/4 ir | z | = sqrt (85) / 2. Atsižvelgiant į tai, kad zs = (1 + 3i) (4-i) / (2 + 2i), mes galime parašyti: | z | ^ 2 = z * zs == (1-3i) (1 + 3i (4 + i) (4-i) / ((2-2i) (2 + 2i)) = (1 + 9) (16 + 1) / (4 + 4) = 85/4 ir | z | = sqrt (85) / 2.
6 patarimas. Kaip pridėti modulį
Modulis - tai yra neatskiriama viso, visko dalis. Modulis gali būti pridėtas arba pašalintas nesunaikinant pagrindinio branduolio. Modulis gali būti programa, prietaiso dalis. Panašus dizainas naudojamas, pavyzdžiui, "Linux" operacinėje sistemoje. Modulinė architektūra turi "Linux" branduolį.

Jums reikės
- - kompiuteris;
- - Linux operacinė sistema.
Instrukcijos
1
Norėdami pridėti arba pašalinti modulius "Linux" operacinėje sistemoje, yra specialios komandos ir "modprobe" programa. "Linux" branduolyje yra daug kodų, kurie palaiko vieną ar kitą vertę.
2
Visi moduliai yra specialioje kataloge/ lib / modules / $ (uname -r). Pridėti arba pašalinti modulį iš "Linux" branduolio su komanda modprobe. Pirmiausia įveskite vartotojo slaptažodį ir prisijunkite kaip administratorius.
3
Standartinė komandinės eilutės eilutėkodas atrodo maždaug taip: [leh @ localhost leh] #. Komanda pridėti modulius turi būti įvesta taip: sudo modprobe vboxdrv. Tada raskite reikiamą modulį savo „Linux“ sistemoje.
4
Visi pagrindiniai moduliai turi būti įkeltiautomatiškai. Jei, įdiegus bet kokią aparatūrą, vis tiek reikia pridėti branduolio modulį, Kudzu programa turėtų būti paleista. Ji nustatys, ar ši įranga palaiko sistemą, ir sukonfigūruoti jos modulį. Norėdami sužinoti, ar modulis sėkmingai pridėtas, naudokite komandą / sbin / lsmod.







